Rabbit Algebra

From Homestar Runner Wiki

(Difference between revisions)
Jump to: navigation, search
(LaTeX formatting)
Line 4: Line 4:
==Fun Facts==
==Fun Facts==
-
*If solved, ''x'' = ±9.
+
*If solved, <math>x = \pm 9</math>
-
*The score, log<sub>''x''</sub>14, is dependent on ''x''
+
*The score, <math>\log_x 14</math>, is dependent on ''x''
**Setting ''x'' to 14 or any integer root of 14 (e.g. square root, cube root, etc) yields an integral score.
**Setting ''x'' to 14 or any integer root of 14 (e.g. square root, cube root, etc) yields an integral score.
-
**If ''x'' = 9 ''(see above)'', the score is 1.2011.
+
**If <math>x = 9</math> ''(see above)'', the score is 1.2011.
-
**If ''x'' = –9, the score is the [[wikipedia:complex number|complex number]] 0.3945 – 0.5641''i''.
+
**If <math>x = - 9</math>, the score is the [[Wikipedia:Complex number|complex number]] <math>0.3945 - 0.5641i</math>.
-
**If ''x'' = 3 ''(see below)'', the score is 2.4022.
+
**If <math>x = 3</math> ''(see below)'', the score is 2.4022.
**The score cannot be zero.
**The score cannot be zero.
-
*In the number of "mans", 2''x''=6, ''x'' is equal to 3.
+
*In the number of "mans", <math>2x = 6</math>, ''x'' is equal to 3.
-
*The version on HomestarRunner.com PAY PLUS! has the problem ''x''<sup>2</sup> + 28 = 44, which gives ''x'' = &plusmn;4.
+
*The version on [[HomestarRunner.com PAY PLUS!]] has the problem <math>x^2 + 28 = 44</math>, which yields <math>x = \pm 4</math>
==Appearances==
==Appearances==

Revision as of 19:25, 4 December 2006

Solve for X!!

Rabbit Algebra is a Videlectrix educational title, shown in the Peasant's Quest Preview. It is a "game" where algebra is taught by a rabbit. This is a parody of The Learning Company's Reader Rabbit and Math Rabbit, where various animals teach elementary subjects. It is not listed on Videlectrix's website and cannot be played.

Fun Facts

  • If solved, x = \pm 9
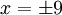
  • The score, logx14, is dependent on x
    • Setting x to 14 or any integer root of 14 (e.g. square root, cube root, etc) yields an integral score.
    • If x = 9 (see above), the score is 1.2011.
    • If x = − 9, the score is the complex number 0.3945 − 0.5641i.
    • If x = 3 (see below), the score is 2.4022.
    • The score cannot be zero.
  • In the number of "mans", 2x = 6, x is equal to 3.
  • The version on HomestarRunner.com PAY PLUS! has the problem x2 + 28 = 44, which yields x = \pm 4

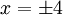
Appearances


Videlectrix Games
Games Menu50K Racewalker, Awexome Cross, Duck Guardian One, Hallrunner, Kid Speedy, Peasant's Quest, Pigs on Head, Population: Tire, RhinoFeeder, Secret Collect., Stinkoman 20X6, StrongBadZone, TROGDOR!, Thy Dungeonman, Thy Dungeonman 2, Thy Dungeonman 3, Where's an Egg?
SBCG4APStrong Bad's Cool Game for Attractive People
Homestar Ruiner (Snake Boxer 5), Strong Badia the Free (Math Kickers), Baddest of the Bands (Limozeen's Hot Babelien Odyssey), Dangeresque 3: The Criminal Projective (Space Circus Catastrophe), 8-Bit is Enough (Gel-Arshie's Pro Fruitboarder)
itch.ioDangeresque: The Roomisode Triungulate (Behind the Dangerdesque; The Intersection of Doom & Boom (Rig Rug); Keep My Enemies, Loser; Inspection Certificate on File in Building Office), Halloween Hide & Seek, Marzipan Beef Reverser, Trogday Micro Game (Burninate the Barnyard)
OtherDuck Pond, Where's The C.H.E.A.T.
Non-playable Butcher Bros., C.H.E.A.T., Cheat Commandos Tactics, Duck Guardian 2, Fluffy Puff Mayonnaise Game, Halfathlon, King Dingo, Lewis Rudkin SX: england, Planet Alert!, QWERTY, Rabbit Algebra, Salad Daze, Shploitz!, Spaceshipper, Spirits of '76, Sundae Drivin', Trogdor: Let's Burninate Phonics
See Also Videlectrix Guys, Videlectrix Mascot, videlectrix.itch.io, videlectrix.com, Viidelectrix
Retrieved from "http://www.hrwiki.org/wiki/Rabbit_Algebra"
Personal tools